Cryptography(암호학) - RSA(공개키 암호)
RSA 암호 알고리즘은 대표적인 공개키 암호 알고리즘이다.(공개키 알고리즘 : https://hackhijack64.tistory.com/60)
RSA 암호 알고리즘은 아주 큰 두 소수의 곱으로 이루어진 합성수 인수분해 문제의 어려움을 이용한 암호이다. 따라서 RSA로 암호화할 때는 합성수의 소인수분해가 어려워지도록 각 인자를 적절히 설정 해야한다.
RSA는 공개키와 개인키로 이루어져 있다.
공개키는 모두에게 공개되어 있고, 암호화에 사용된다.
개인키는 아무한테도 노출되면 안되고, 암호를 복호화 할때 사용된다.
먼저 RSA를 이해하려면 오일러 정리를 알아야한다.
오일러 정리는 n과 서로소인 양의 정수 m과 다음 식이 성립된다는 것이다.

P(n)은 오일러 파이 함수라고 하며, n이하의 양의 정수중 서로소인 수의 개수를 나타낸다.
EX. P(10) : (1,10), (3,10), (7,10), (9,10) : 4가 된다.
그럼 소수 p는 1부터 p까지 모두 서로소 라서, P(p) = p-1된다.
이제 RSA의 과정을 알아보자.
일단 1024비트 이상의 소수 p,q를 각각 정한다.
그리고 아래를 계산하여 n을 생성한다.
n = p x q
그러면 P(n)은 n에서 p의 배수 q개, q의 배수 p개, 그리고 최소공배수 n, 1개를 빼서 계산할 수 있다.
P(n) = n - p - q - 1 = p x q - p - q + 1 = (p-1)(q-1)
그리고 P(n)보다 작은 서로소 e를 정한다.
그러면 아래의 식으로 d를 구한다.
d ≡ 1/e mod P(n)
그러면 이 중, n과 e는 공개키, d는 개인키로 사용된다.
이제 암호화, 복호화 과정을 알아보자.
평문을 T라고 하면 아래의 공식으로 암호화가 진행된다.(암호문 : C)
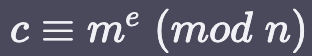
그리고 복호화는 다음 식으로 진행된다.
