728x90
반응형
반응형
이번에는 드림핵의 암호 문제인 ICM2022를 풀어볼 것이다.
문제코드는 아래와 같다.
import random
from fractions import Fraction
def enc(p, n, key1, key2):
q = (Fraction(p, n+1)*key1**(n+1)) - (Fraction(p, n+1)*key2**(n+1))
print("[OK] plain is encrypted : ", q)
return q
def dec(q):
# cencored
def key_make():
n, key1, key2 = 0, 1, 0
while key2 < key1:
n = random.randrange(1, 10) #3
key1 = random.randrange(1, 100) #
key2 = random.randrange(1, 100) #95
return n, key1, key2
p = ""
emp = input("plain text: ")
for character in emp:
p += str(ord(character))
n, key1, key2 = key_make()
print(f"[WAR]p = {p} n = {n} key1 = {key1} key2 = {key2}")
q = enc(int(p), n, key1, key2)
dec(q)
일단 코드를 해석을 잠시 하자면 p라는 문자열을 받아서 아스키코드로 바꾸고 이 값을 가지고 enc() 함수에서 아래와 같이 연산한다.

여기서 q, n, key2가 주어져서 알기 때문에 아래와 같이 나타낼 수 있다.
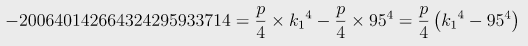
그럼 이를 p에 관해서 정리해주면 아래와 같다.
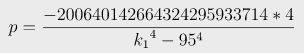
여기서 k1은 k2보다 작고, 1에서 100 중 난수가 나오니깐, k1의 4제곱 - 95의 4제곱이 q * 4에 나누어 떨어질 때까지 k1의 값을 brute forcing 하면 된다.
이를 파이썬으로 구현하면 아래와 같다.
from fractions import Fraction
re = list()
for i in range(1,95):
k2 = 95 ** 4
k1 = i ** 4
result = k1 - k2
re.append(result)
for i in re:
q = -200640142664324295933714 * 4
p = Fraction(q/i)
if q % i == 0 :
print(p)이를 실행하면 아래와 같이 p(flag)값이 나오는 걸 확인할 수 있다.

728x90
반응형
'Cryptography' 카테고리의 다른 글
| Dreamhack - d (writeup) (0) | 2023.02.22 |
|---|---|
| Dreamhack - Robot Only(writeup) (0) | 2023.02.22 |
| Dreamhack - darimchal_001(writeup) (0) | 2023.02.22 |
| Cryptography(암호학) - Hash(해시) (0) | 2021.12.26 |
| Cryptography(암호학) - RSA(공개키 암호) (0) | 2021.12.23 |
